損益分岐点売上高算出の公式
前講でご紹介したように、損益分岐点売上高(=損益がプラスマイナスゼロになる売上高)がいくらなのかを求めるには、まず損益分岐点販売数量を求めてから販売単価を掛けて算出する方法を学習しました。
ところが、問題によっては、損益分岐点販売数量が割り切れない数字になったり、あるいは、売上高や変動費が総額で与えられて、製品1個当たりの貢献利益が分からないという設定の場合もあります。
そこで、いきなり損益分岐点売上高から先に算出する公式をご紹介します。

分子が「固定費」になっているのは、損益分岐点販売数量の場合の公式と同じですが、分母が「貢献利益率」となっています。
この貢献利益率とは何でしょうか?
前講のリンゴの例(1個¥40で仕入、¥100で販売、固定費¥300,000)で考えていきます。

上表のように、1個¥40で仕入れて¥100で売れば、一旦¥60の儲けが出ますが(=貢献利益)、固定費を引いた数字が最終の営業利益でした。2個売れば売上高は¥200、変動費¥80、貢献利益¥120でした。
方程式を使った、損益分岐点売上高の求め方
ここで文字式を使って、売上高をS(円)と置きます。
すると、変動費はSを使って、どのように表されるでしょうか?
この設例では、変動費(仕入れ値)は必ず売上高の4割になっていますから、
変動費=0.4S
と表されます。このとき、この0.4のことを「変動費率」といいます。
では同じように、貢献利益は売上高Sを使って、どのように表されるでしょうか?
この設例では、貢献利益は売上高Sから、変動費0.4Sを引いたものですから、
貢献利益=0.6S
と表されます。このとき、この0.6のことを「貢献利益率」といいます。
ところで、リンゴ1個売り上げた場合の営業利益の計算式と同様に、売上高Sの場合の営業利益の計算式を並べてみると・・・
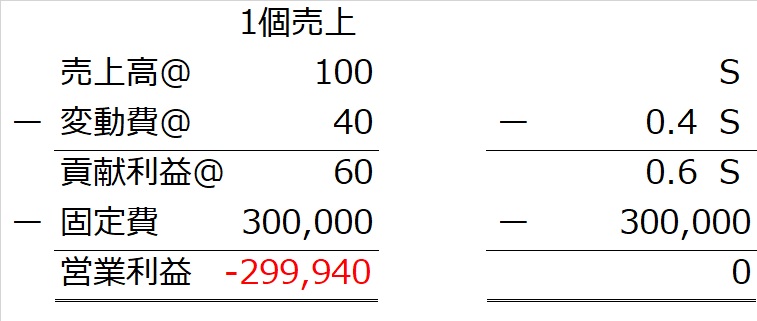
営業利益ゼロのときが、損益分岐点なわけですから、このときのSがいくらになるのか、を解いていけば、損益分岐点売上高が計算されるわけです。
上の式でいうと、「貢献利益0.6S-固定費300,000=0」の一元一次方程式を解けば、損益分岐点売上高が出ます。
「-300,000」を式の右辺に移項して、式全体を0.6で割れば、
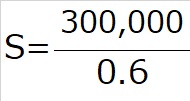
上の式を眺めていて、何か気が付きませんか?
これが、冒頭にご紹介した損益分岐点売上高算出の公式

になっています。
これを解けば、S=500,000
つまり、今回の設例の場合の損益分岐点売上高は¥500,000と算出されました。
損益分岐点販売数量は?
では、先に損益分岐点売上高を出してから、次に損益分岐点販売数量を出すには、どうやって計算すればいいでしょうか?
トータルの売上高¥500,000を、1個当たりの売値(販売単価)¥100で割れば、数量が出ますね。
売上高¥500,000÷1個当たり販売単価@¥100/個=5,000個
これが損益分岐点販売数量です。前講で出した数量と同じです。
方程式を使った、損益分岐点販売数量の求め方
この損益分岐点販売数量も、X個とおいて、文字式を使って算出することができます。
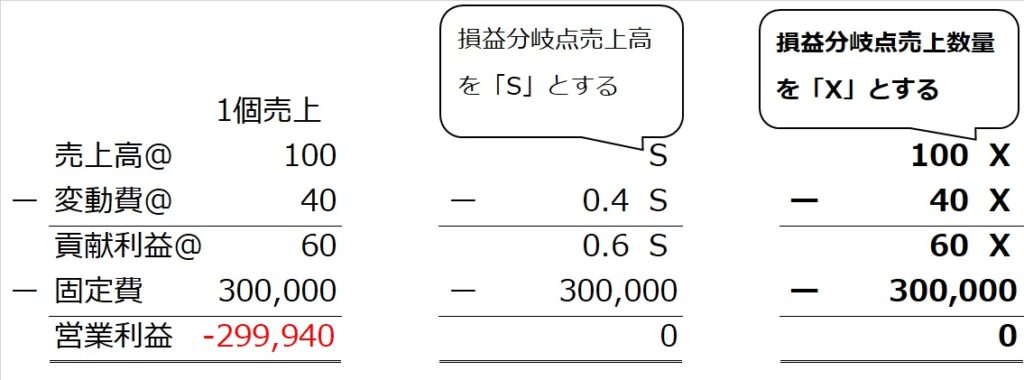
数量をXと置くと、売上高は100X、変動費は40X、貢献利益は60Xと表されるのはわかりますか?
あとは、「60X-300,000=0」の方程式をXについて解けばいいわけですね。
「-300,000」を式の右辺に移項して、式全体を60で割れば、
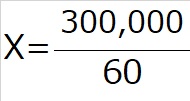
このとき、300,000が固定費、60が1個当たり貢献利益でしたから、
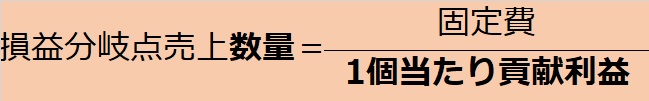
前講で覚えた公式になっています。
以上のように、売上高をS,数量をXというように文字式・方程式を使う方法が汎用性もあって応用ができるのでいいのですが、方程式の立て方そのものを思い出すのに時間がかかる方は、損益分岐点売上高・損益分岐点販売数量の算出公式を、できれば両方、最悪どちらか一方を試験で思い出せるようにしておいてください。